Purpose:
Determine a relationship for the repulsive force between two identical magnets while also verifying that conservation of energy applies to magnetic fields.
Theory:
Forces due to gravitational and electric fields follow an inverse square law. Since magnetic forces also behave similarly in that they exert a force in a field, it is believed that a magnetic force should also behave according to some inverse power of distance in the form F=C(r^n) where C is an experimental constant for some particular situation, r is the distance between the magnets, and n is an experimental constant. By graphing measurements of force on one magnet and the resulting distance between the magnets, a model can be produced to predict the magnetic force at various distances r. As our experiment involves repulsive magnetic forces, we may test conservation of energy by graphing the motion of an object as it moves towards the magnet and finding the velocities at which it approaches and then retreats after being repelled.
Apparatus:
- Strong magnet (2)
- Air track and cart
- Motion detector
- Digital scale
- Angle measurement device
Procedure:
Attach one magnet to the cart and one magnet to one end of the air track, facing towards the cart. Tilt the air track and measure its degree of inclination. With the air track on, release the cart and allow it to reach an equilibrium position. Measure the distance between the magnet on the cart and the magnet attached to the track. Repeat these steps for a total of 6 different angle measurements. Level the track and orient the two magnets towards each other at some relatively short distance. Measure the distance between the motion sensor and the area of the cart from which position is measured and measure the distance between the two magnets. Subtract the distance between the magnets from the distance between the cart and the motion detector to obtain a value used to convert position as measured by the motion sensor to distance between the magnets. With the air track on, slide the cart towards the fixed magnet and produce a graph of velocity vs time.
Data and Graphs:
Photo of experimental setup
Sample calculation of gravitational force equated to magnetic force
Fgrav = Fmagnet = Mcart*G*sin(θ) = 0.354*9.81*sin(0.035) = 0.118N
Sample calculation of magnetic potential energy Umagnet
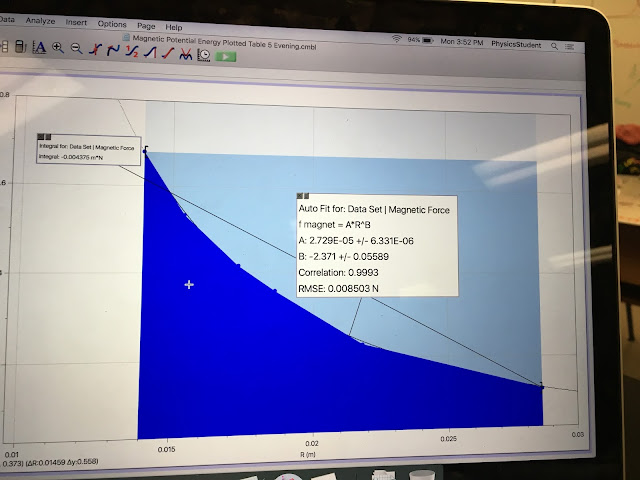
Umagnet = integral F(r)dr = integral (2.729*10^-5)/(r^-2.371) = (-2.29*10^-5)/(1.371*(r^-1.371))
Sample calculation of distance between magnets r, used to create PE graph
r = measured position (from detector) - constant value = 20cm - 10.6cm = 9.4cm
Table of collected data and calculated values
Data and Graphs:
Photo of experimental setup
Sample calculation of gravitational force equated to magnetic force
Fgrav = Fmagnet = Mcart*G*sin(θ) = 0.354*9.81*sin(0.035) = 0.118N
Sample calculation of magnetic potential energy Umagnet
Umagnet = integral F(r)dr = integral (2.729*10^-5)/(r^-2.371) = (-2.29*10^-5)/(1.371*(r^-1.371))
Sample calculation of distance between magnets r, used to create PE graph
r = measured position (from detector) - constant value = 20cm - 10.6cm = 9.4cm
Table of collected data and calculated values
| Mass | 345 | g | |
| θ (°) | r (cm) | θ (rad) | Fgrav (N) |
| 2,0 | 2,86 | 0,035 | 0,118 |
| 3,8 | 2,18 | 0,066 | 0,224 |
| 5,9 | 1,86 | 0,103 | 0,348 |
| 6,9 | 1,73 | 0,120 | 0,407 |
| 8,8 | 1,54 | 0,154 | 0,518 |
| 11,3 | 1,40 | 0,197 | 0,663 |
Graph of kinetic, potential, and total energy (above) and of velocity (below)
Data Analysis:
The graph of force vs radius produced the experimental constants for our equation for magnetic force. Using LoggerPro's power fit ability, an equation was produced for the curve. The constant value C is equal to 2.729*10^-5 and the power n is equal to -2.371. Using the new equation of F=2.729*10^-5r^(-2.371), the total magnetic potential energy was calculated using the integral of force with respect to distance. From the velocity graph, a graph of kinetic energy vs time was produced. Using our equation for magnetic potential energy, a graph of potential energy vs time was produced. Total energy was then found by adding kinetic and potential energy.
Conclusion:
The model produced for magnetic force was F=2.729*10^-5r^(-2.371) where r is the distance between two repelling magnets. This matches our prediction of an inverse power relationship between magnetic force and distance. Using this equation, the total potential energy shown in the first graph was calculated at 4.17*10^-3J. Based on the graphs produced of KE, PE, and total energy, it was concluded that energy is conserved in magnetic potential energy since no sudden decrease in total energy was observed. The gradual decrease in total energy is due to slight friction and air resistance as the cart moved along the track. Although calculations were not made to determine the exact total energy before and after the magnetic repulsion, it is assumed that these frictional forces are responsible for the slight decrease in total energy during the magnetic repulsion.


No comments:
Post a Comment